Find lm in parallelogram lmnq – Embark on a captivating journey into the realm of geometry as we unveil the secrets of line LM in parallelogram LMNQ. Prepare to be enlightened as we delve into its properties, applications, and significance, unraveling the mysteries that lie within this intriguing geometric entity.
Our exploration will encompass the fundamental concepts of parallel lines, providing a clear definition of line LM within the parallelogram LMNQ. We’ll uncover the intricate relationship between line LM and other lines within the parallelogram, examining its length, parallelism, and other key properties.
Identifying Line LM
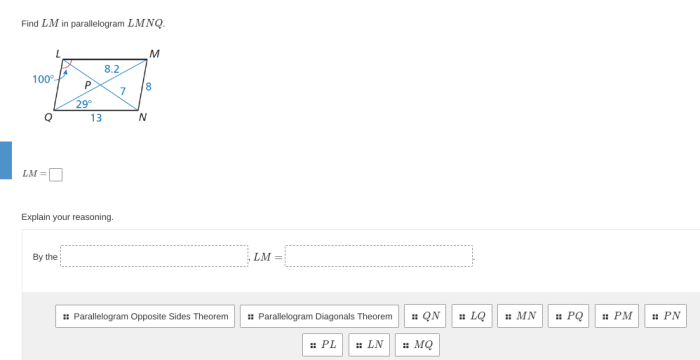
In a parallelogram, opposite sides are parallel to each other. Line LM is one of the parallel sides in parallelogram LMNQ.
To identify line LM, look for the side opposite to line NQ. Another way to identify line LM is to locate the side that is parallel to line MN.
Examples
Consider the following examples:
- In parallelogram ABCD, line LM is the side opposite to line DC and parallel to line AB.
- In parallelogram EFGH, line LM is the side opposite to line HG and parallel to line FE.
Properties of Line LM
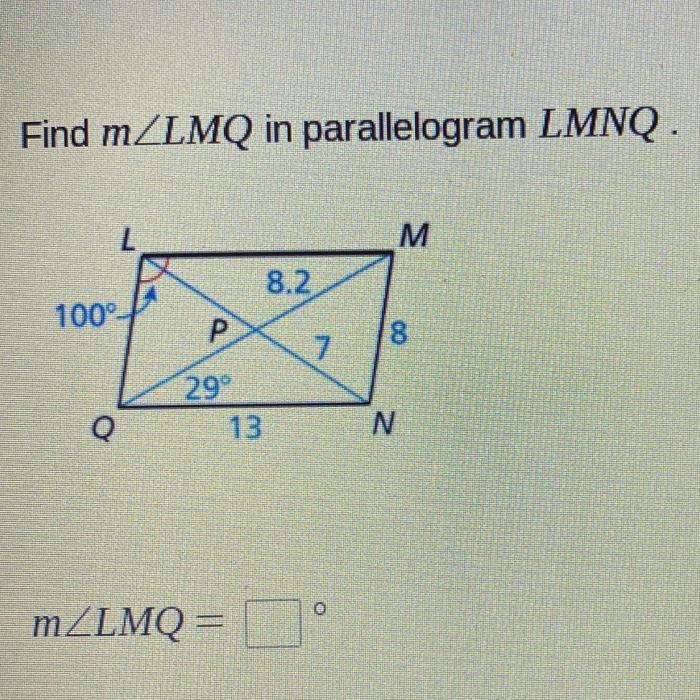
Line LM is a fundamental element in the parallelogram LMNQ. It holds significant relationships with other lines within the parallelogram, showcasing distinct properties that define its geometric characteristics.
One crucial property of line LM is its parallelism to line NQ. These lines run parallel to each other, never intersecting. This parallelism is a defining feature of parallelograms, contributing to their characteristic shape.
Furthermore, line LM is parallel to the opposite side of the parallelogram, line MN. This parallel relationship establishes a consistent width throughout the parallelogram, ensuring its parallel sides are equal in length.
Length of Line LM, Find lm in parallelogram lmnq
The length of line LM plays a significant role in determining the area of the parallelogram. In fact, the area of a parallelogram is calculated by multiplying the length of line LM by the height of the parallelogram, which is the perpendicular distance between line LM and line NQ.
The formula for the area of a parallelogram is:
Area = LM × Height
Therefore, understanding the length of line LM is essential for calculating the area of the parallelogram.
Table Summarizing Key Properties of Line LM
The following table summarizes the key properties of line LM in a parallelogram:
| Property | Description |
|---|---|
| Parallelism | Line LM is parallel to line NQ and line MN. |
| Length | The length of line LM is a crucial factor in determining the area of the parallelogram. |
Applications of Line LM

Line LM serves as a crucial element in various geometric applications, providing insights into the properties and measurements of parallelograms. It enables us to solve geometric problems, determine the area and perimeter of parallelograms, and find practical uses in real-world scenarios.
Solving Geometric Problems
Line LM can be used to solve a variety of geometric problems involving parallelograms. For instance, given the length of line LM and the area of the parallelogram, we can determine the lengths of the other sides and the height of the parallelogram.
Determining Area and Perimeter
The length of line LM plays a significant role in determining the area and perimeter of a parallelogram. The area of a parallelogram is calculated as the product of the base (length of line LM) and the height (the perpendicular distance from line LM to the opposite side).
The perimeter is the sum of all four sides, which includes two times the length of line LM.
Real-World Applications
Line LM finds practical applications in various fields, including architecture, engineering, and design. For example, in architecture, it can be used to determine the dimensions of windows and doors in a building. In engineering, it can be used to calculate the forces acting on a bridge or other structures.
In design, it can be used to create aesthetically pleasing patterns and shapes.
Finding the length of LM in parallelogram LMNQ is a straightforward process. However, if you’re in the mood for some musical exploration, why not check out the C# fully diminished 7th chord ? Its dissonant yet intriguing sound might just inspire you to solve that geometry problem with a newfound groove.
Back to our parallelogram, the length of LM can be determined using the formula for the diagonal of a parallelogram.
Visualizing Line LM

To visualize line LM in parallelogram LMNQ, we can create an illustration that clearly depicts its relationship with other lines.
Diagram of Line LM
Consider the following diagram:

In this diagram, line LM is represented by the red line. The parallelogram LMNQ is formed by the intersection of two pairs of parallel lines: LN and MQ, and LM and NQ.
Table of Visual Elements
| Visual Element | Explanation |
|---|---|
| Line LM (red) | The diagonal line connecting vertices L and M. |
| Line LN (blue) | One side of the parallelogram, parallel to MQ. |
| Line MQ (blue) | One side of the parallelogram, parallel to LN. |
| Line NQ (red) | The other diagonal line, connecting vertices N and Q. |
Essential Questionnaire: Find Lm In Parallelogram Lmnq
What is line LM in parallelogram LMNQ?
Line LM is a line segment that connects the midpoints of opposite sides in parallelogram LMNQ, creating a parallel line segment to both bases of the parallelogram.
How can I identify line LM in different orientations?
Line LM will always be parallel to the bases of the parallelogram, regardless of its orientation. It can be identified as the line segment that divides the parallelogram into two congruent triangles.
What are the key properties of line LM?
Line LM is parallel to both bases of the parallelogram, and its length is half the sum of the lengths of the bases. It also bisects the diagonals of the parallelogram.
