Parallel Lines And Transversals Project

Parallel lines and transversals project – The realm of geometry unveils its secrets in this comprehensive examination of parallel lines and transversals, inviting us to unravel their intricate relationships and practical applications. Delving into the depths of this mathematical tapestry, we will explore the fundamental concepts, theorems, and extensions that define these geometric constructs, illuminating their significance in the wider world of geometry and beyond.

As we embark on this journey, we will encounter the foundational definitions of parallel lines and transversals, gaining a clear understanding of their unique properties. Theorems such as the Alternate Interior Angles Theorem, Corresponding Angles Theorem, and Same-Side Interior Angles Theorem will be meticulously explained, revealing the intricate connections between these geometric principles.

Definition of Parallel Lines and Transversals

In geometry, parallel lines are lines that never intersect, no matter how far they are extended. Transversals are lines that intersect two or more parallel lines.

Parallel lines are represented by the symbol ∥, and transversals are represented by the symbol ⊥. The intersection of a transversal and a parallel line is called a point of intersection.

Properties of Parallel Lines and Transversals

Parallel lines are always equidistant from each other.
Transversals intersect parallel lines at the same angle.
The alternate interior angles formed by a transversal intersecting two parallel lines are congruent.
The corresponding angles formed by a transversal intersecting two parallel lines are congruent.
The same-side interior angles formed by a transversal intersecting two parallel lines are supplementary.

Theorems Related to Parallel Lines and Transversals

Alternate Interior Angles Theorem, Parallel lines and transversals project

The Alternate Interior Angles Theorem states that if a transversal intersects two parallel lines, then the alternate interior angles are congruent.

In the diagram below, ∠1 and ∠5 are alternate interior angles. Since lines l and m are parallel, ∠1 ≅ ∠5.

[Diagram of parallel lines l and m intersected by a transversal t, showing alternate interior angles ∠1 and ∠5]

Corresponding Angles Theorem

The Corresponding Angles Theorem states that if a transversal intersects two parallel lines, then the corresponding angles are congruent.

In the diagram below, ∠2 and ∠6 are corresponding angles. Since lines l and m are parallel, ∠2 ≅ ∠6.

[Diagram of parallel lines l and m intersected by a transversal t, showing corresponding angles ∠2 and ∠6]

Same-Side Interior Angles Theorem

The Same-Side Interior Angles Theorem states that if a transversal intersects two parallel lines, then the same-side interior angles are supplementary.

In the diagram below, ∠3 and ∠7 are same-side interior angles. Since lines l and m are parallel, ∠3 + ∠7 = 180°.

[Diagram of parallel lines l and m intersected by a transversal t, showing same-side interior angles ∠3 and ∠7]

Applications of Parallel Lines and Transversals: Parallel Lines And Transversals Project

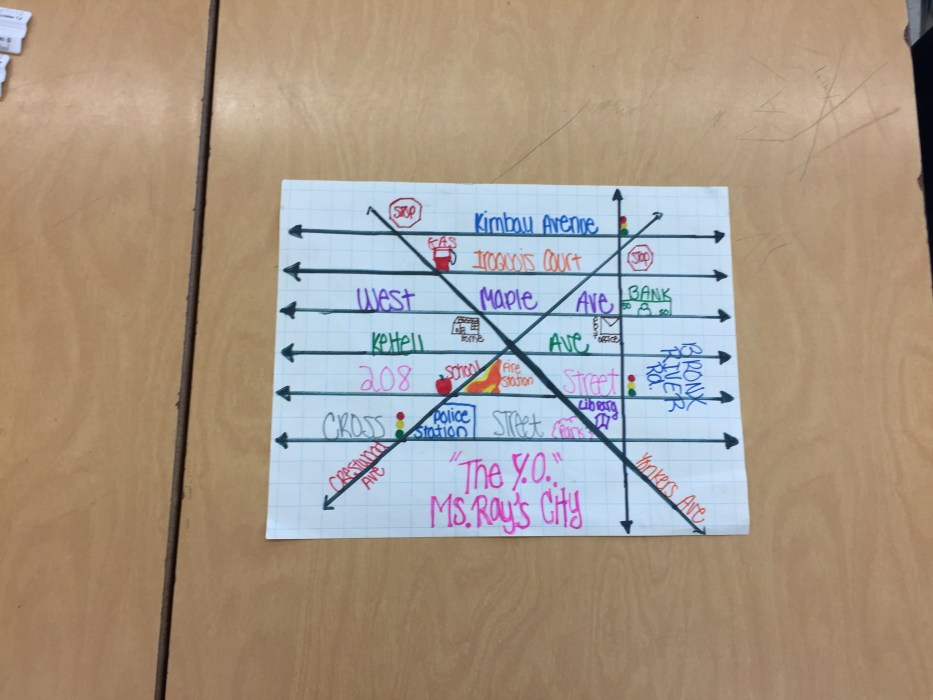
Parallel lines and transversals are used in a variety of applications in geometry, architecture, engineering, and design.

In architecture, parallel lines are used to create the illusion of space and depth. For example, the columns in a colonnade are often parallel to each other, which makes the space appear larger and more impressive.
In engineering, parallel lines are used to create structures that are strong and stable. For example, the beams in a bridge are often parallel to each other, which helps to distribute the load evenly and prevent the bridge from collapsing.
In design, parallel lines are used to create a sense of order and balance. For example, the stripes on a flag are often parallel to each other, which creates a visually appealing design.

Proof Techniques for Parallel Lines and Transversals

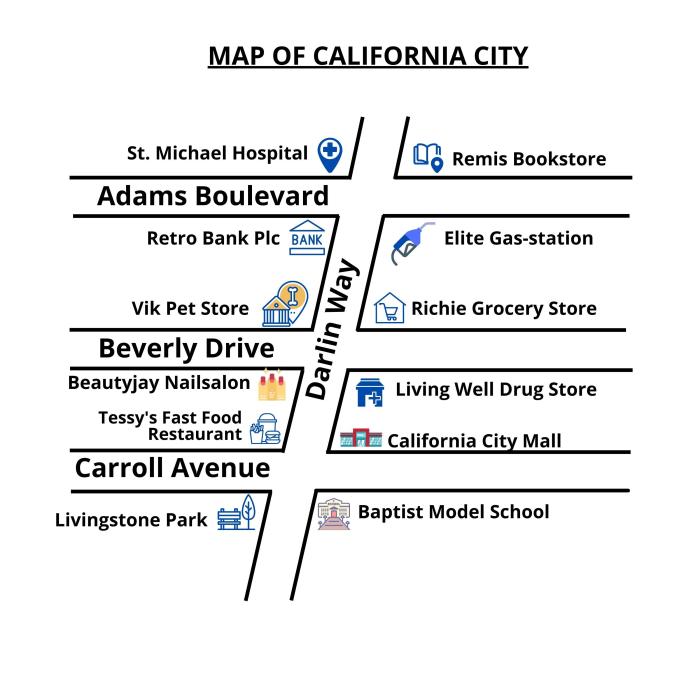
There are a number of methods that can be used to prove that lines are parallel or perpendicular.

The Angle Sum Theorem can be used to prove that two lines are parallel if the sum of the interior angles on one side of a transversal is 180°.
The Converse of the Angle Sum Theorem can be used to prove that two lines are perpendicular if the sum of the interior angles on one side of a transversal is 90°.
The Corresponding Angles Theorem can be used to prove that two lines are parallel if the corresponding angles formed by a transversal are congruent.
The Alternate Interior Angles Theorem can be used to prove that two lines are parallel if the alternate interior angles formed by a transversal are congruent.
The Same-Side Interior Angles Theorem can be used to prove that two lines are parallel if the same-side interior angles formed by a transversal are supplementary.

Extensions of Parallel Lines and Transversals

The concept of parallel lines and transversals can be extended to include angle bisectors and parallelograms.

An angle bisector is a line that divides an angle into two congruent angles.
A parallelogram is a quadrilateral with opposite sides parallel.

The properties of angle bisectors and parallelograms can be used to prove a variety of theorems about parallel lines and transversals.

Quick FAQs

What are parallel lines?

Parallel lines are two lines that never intersect, no matter how far they are extended.

What is a transversal?

A transversal is a line that intersects two or more other lines.

What is the Alternate Interior Angles Theorem?