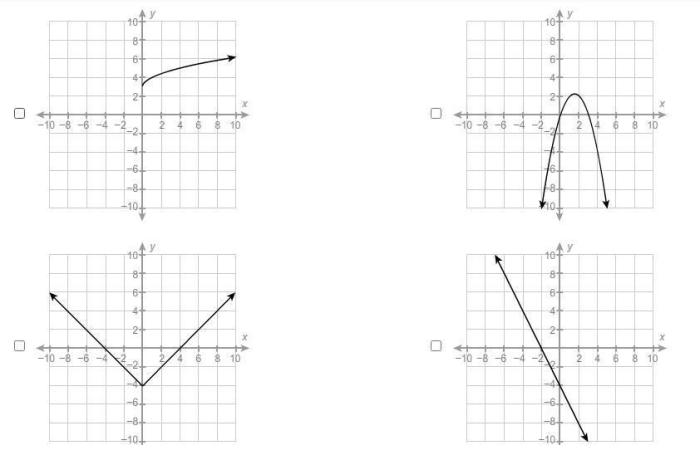
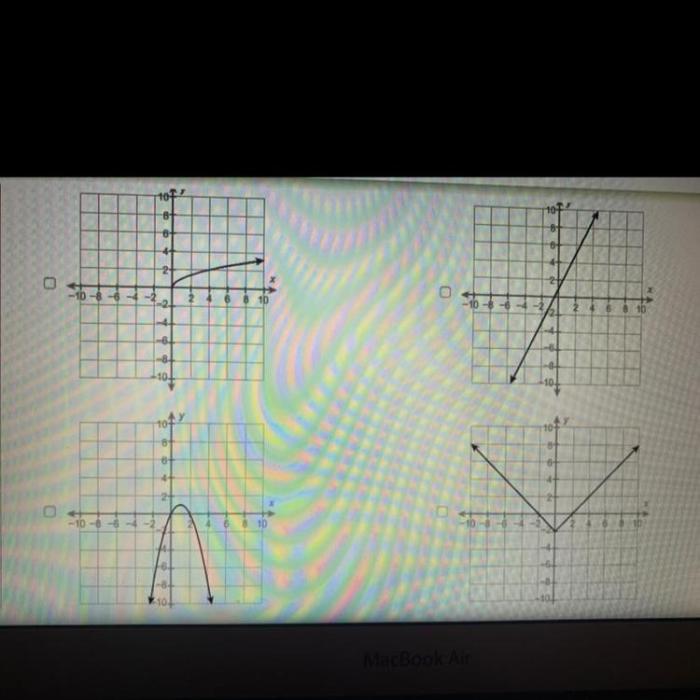
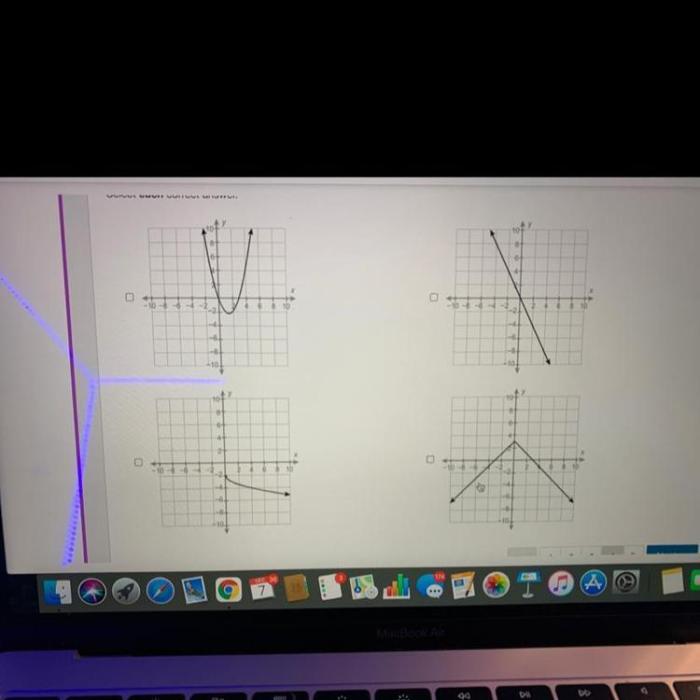
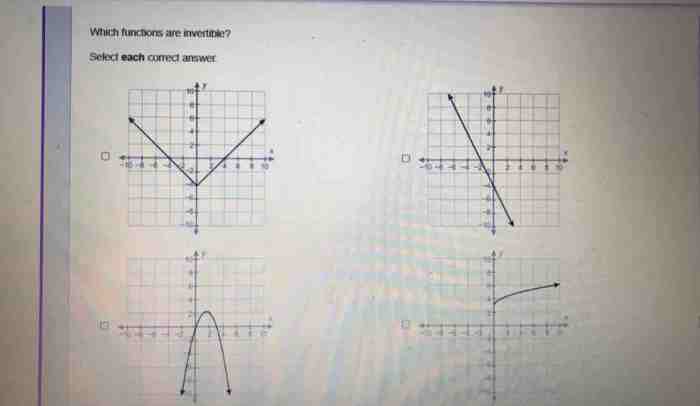
Which functions are invertible select each correct answer – In mathematics, a function is invertible if there exists a function that undoes the original function. In other words, if f(x) = y, then the inverse function, f^(-1)(y), will give you back x. Not all functions are invertible, however. In this article, we will explore the concept of invertibility and discuss which functions are invertible and which are not.
A function is invertible if and only if it is one-to-one and onto. A function is one-to-one if each element in the domain is mapped to a unique element in the range. A function is onto if every element in the range is mapped to by at least one element in the domain.
Functions and Invertibility
A function is a relation that assigns to each element of a set a unique element of another set. The inverse of a function is a function that reverses the mapping of the original function. In other words, if $f(x)$ is a function, then its inverse $f^-1(x)$ is the function such that $f^-1(f(x)) = x$ and $f(f^-1(x)) = x$.
Not all functions are invertible. A function is invertible if and only if it is one-to-one and onto. A function is one-to-one if no two distinct elements of the domain map to the same element of the range. A function is onto if every element of the range is mapped to by at least one element of the domain.
Properties of Invertible Functions
- The inverse of an invertible function is also invertible.
- The inverse of the composition of two invertible functions is equal to the composition of the inverses of the two functions in reverse order.
- If a function is invertible, then its graph is symmetric about the line $y = x$.
Methods for Finding Inverse Functions, Which functions are invertible select each correct answer
There are several methods for finding the inverse of a function, including:
- Algebraic method:This method involves solving the equation $y = f(x)$ for $x$ in terms of $y$.
- Graphical method:This method involves reflecting the graph of the function about the line $y = x$.
Applications of Invertible Functions
Invertible functions are used in a variety of applications, including:
- Cryptography:Invertible functions are used to encrypt and decrypt messages.
- Mathematics:Invertible functions are used to solve equations and to prove theorems.
- Engineering:Invertible functions are used to design and analyze systems.
FAQ: Which Functions Are Invertible Select Each Correct Answer
What is an invertible function?
An invertible function is a function that can be undone. In other words, if f(x) = y, then the inverse function, f^(-1)(y), will give you back x.
What are the properties of invertible functions?
Invertible functions are one-to-one and onto. A function is one-to-one if each element in the domain is mapped to a unique element in the range. A function is onto if every element in the range is mapped to by at least one element in the domain.
How do you find the inverse of a function?
There are a few different methods for finding the inverse of a function. One method is to use the algebraic method. Another method is to use the graphical method.